梯度下降

# 什么是梯度下降

梯度下降是一种优化算法，常用于训练机器学习 (opens new window) 模型和神经网络 (opens new window)。训练数据可以帮助这些模型不断学习，梯度下降算法中的成本函数就像是晴雨表，通过每次参数更新的迭代来衡量模型的准确度。该模型持续调整其参数，直至该函数接近于或等于零，以使产生的误差尽可能最小。机器学习模型的准确性经过优化后，这些模型就可以成为人工智能 (AI) 和计算机科学应用的强大工具。

# 梯度下降算法如何工作

在我们深入研究梯度下降算法之前，回顾一下线性回归中的一些概念可能会有所帮助。大家可能还记得直线斜率公式$y=mx+b$，其中 m 表示斜率，b 表示直线在 y 轴上的截距。

大家也可能还记得在统计方法中如何绘制散点图并找到最佳拟合线的过程，这需要使用均方误差公式计算实际输出和预测输出（y 的拟合值）之间的误差。梯度下降算法也与此类似，但它基于凸函数。

梯度下降算法的起点可以是我们评估性能的任意点。我们通过这个起点求出导数（或斜率），可以用切线来观察斜率的大小。斜率将促使一些参数更新，包括权重和偏差。起始点处的斜率比较大，但随着新参数的生成，斜率会逐渐减小，直至达到曲线上的最低点，即收敛点。

与在线性回归中寻找最佳拟合线类似，梯度下降算法的目标是使成本函数最小化，即最大程度减小预测值与实际值之间的误差。为了做到这一点，需要两个数据点 — 一个是方向，另一个是学习速率。这些因素决定了未来迭代的偏导数计算，使其逐渐达到局部或全局最小值（即收敛点）。

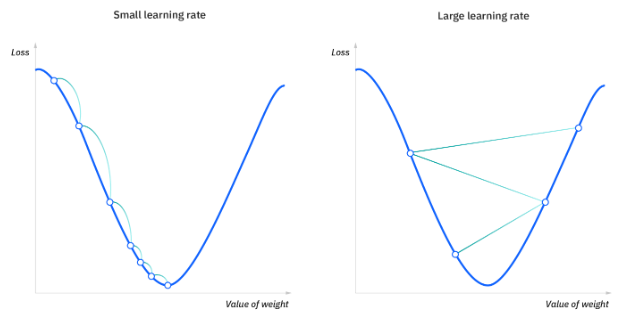
学习速率（也称为步长或 alpha）指的是为了达到最小值所采用的步长的大小。这通常是一个很小的值，根据成本函数的行为进行求值和更新。较高的学习速率会产生较大的步长，存在错过最小值的风险。相反，较低的学习速率的步长较小。虽然较低的学习速率具有更高的精度，但迭代次数的增加会降低整体效率，因为需要更多的时间和计算才能达到最小值。
成本（或损失）函数用于衡量实际值和预测值在当前位置的差异或误差。它通过向模型提供反馈，使其可以调整参数以最大程度减少误差，并找到局部或全局最小值，从而提高机器学习模型的有效性。成本函数会持续迭代，沿着最陡下降方向（负梯度）移动，直到接近或等于零。到达此位置时，模型停止学习。此外，虽然成本函数和损失函数这两个术语被认为是同义词，但它们之间存在细微的差别。值得注意的是，损失函数指的是一个训练示例的误差，而成本函数计算的是整个训练集的平均误差。

# 梯度下降算法的类型

梯度下降学习算法有三种类型：批量梯度下降、随机梯度下降和小批量梯度下降。

# 批量梯度下降算法

批量梯度下降算法对训练集中每个点的误差求总和，只有在所有训练示例都评估后才更新模型。这个过程称为一个训练周期 (training epoc)。

虽然这种批量处理提高了计算效率，但对于大型训练数据集而言，它仍然需要很长的处理时间，因为仍要将所有数据存储到内存中。批量梯度下降算法通常也会产生稳定的误差梯度和收敛性，但有时在寻找局部最小值和全局最小值时，收敛点并不是最理想。

# 随机梯度下降算法

随机梯度下降算法 (SGD) 为数据集中的每个示例运行一个训练周期，并一次性更新所有训练示例的参数。由于只需保存一个训练示例，所以可以更轻松地将它们存储在内存中。虽然这些频繁的更新可以使计算更加详细，速度更快，但与批量梯度下降算法相比，这可能会导致计算效率下降。随机梯度下降算法的频繁更新可能导致嘈杂梯度，但这也有助于避开局部最小值，找到全局最小值。

# 小批量梯度下降算法

小批量梯度下降算法结合了批量梯度下降算法和随机梯度下降算法的理念。它将训练数据集分成小批次，并对每批进行更新。这种方法兼顾了批量梯度下降算法的计算效率和随机梯度下降算法的速度。

# 挑战

虽然梯度下降算法是优化问题的最常见方法，但其本身也面临着一些挑战。其中包括

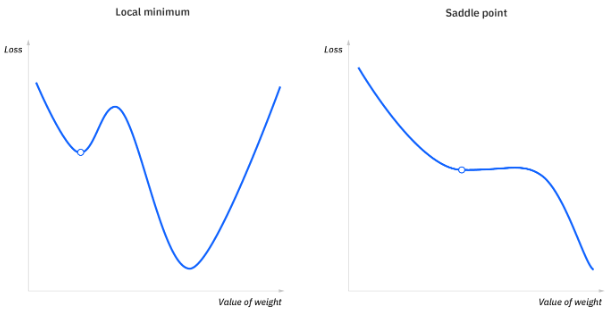
# 局部最小值和鞍点

对于凸问题，梯度下降算法可以很容易地找到全局最小值，但出现非凸问题时，梯度下降算法很难找到全局最小值，而模型只有找到该值才能得到最好的结果。

上文中提到过，当成本函数的斜率等于或接近于零时，模型会停止学习。在一些场景中，除了全局最小值外，局部最小值和鞍点也可能产生这种斜率。在全局最小值处，成本函数的斜率在当前点的任意一侧都会增加，而局部最小值可以模拟全局最小值处的特征。而对于鞍点，负梯度只存在于点的一侧，在一侧达到局部最大值，在另一边达到局部最小值。它的名字来源于马鞍。

嘈杂梯度可以帮助梯度避开局部最小值和鞍点。

# 消失和爆炸梯度

在更深层次的神经网络中，特别是在递归神经网络 (opens new window)中，当使用梯度下降算法和反向传播算法训练模型时，我们还会遇到另外两个问题。

消失梯度： 在梯度过小时发生。当我们在反向传播过程中向后移动时，梯度将持续变小，导致网络中早期层的学习速度比后期层慢。当这种情况发生时，权重参数会进行更新，直到它们变得微不足道 — 即等于零，这将导致算法不再学习。
爆炸梯度： 在梯度太大时会发生这种情况，导致创建的模型不稳定。在这种情况下，模型权重会变得太大，并最终表示为 NaN。解决这个问题的一种方法是利用降维技术，这有助于最大程度地降低模型中的复杂性。

# Tensorflow中的应用

# SGD

# 实例化优化方法： SGD
opt = tf.keras.optimizers.SGD(
    learning_rate=0.1
)
# , momentum=0.0, nesterov=False, name="SGD"
# 定义要调整的参数
var = tf.Variable(1.0)
# 定义损失函数： 无参但有返回值
loss = lambda:(var ** 2)/2.0

# 计算梯度，并对参数进行更新，步长为 `- learning_rate * grad`
opt.minimize(loss,[var])
print(var.numpy()) # 0.9

1
2
3
4
5
6
7
8
9
10
11
12
13

# 动量梯度下降

# 实例化优化方法： SGD
opt = tf.keras.optimizers.SGD(
    learning_rate=0.1,momentum=0.9
)
# , momentum=0.0, nesterov=False, name="SGD"
# 定义要调整的参数
var = tf.Variable(1.0)
var0 = var.numpy()

# 定义损失函数： 无参但有返回值
loss = lambda:(var ** 2)/2.0

# 第一次更新：计算梯度，并对参数进行更新，步长为 `- learning_rate * grad`
opt.minimize(loss,[var])
var1 = var.numpy()

# 第二次更新，并对参数进行更新，因为加入了momentum，因此步长会增加
opt.minimize(loss,[var])
var2 = var.numpy()
# 展示参数更行结果
print("第一次更新步长={}".format((var0-var1)))
print("第二次更新步长={}".format((var1-var2)))
# 第一次更新步长=0.10000002384185791 第二次更新步长=0.18000000715255737

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# Adagrad

# 初始化Adagrad优化器
opt = tf.keras.optimizers.Adagrad(learning_rate=0.1,initial_accumulator_value=0.1,epsilon=1e-06)
# 定义要更新的参数
var = tf.Variable(1.0)
# 定义损失函数
def loss():
    return (var ** 2)/2.0
# 进行更新
opt.minimize(loss,[var])
var.numpy() # 0.9046538

1
2
3
4
5
6
7
8
9
10

# RMSprop

# RMSprop 优化器：Adagrad在迭代后期由于学习率过小，难以找到最优解
opt = tf.keras.optimizers.RMSprop(learning_rate=0.1)
# 定义要更新的参数
var = tf.Variable(1.0)
# 进行更新
opt.minimize(loss,[var])
var.numpy() # 0.6837723

1
2
3
4
5
6
7

# Adam

# Adam
opt = tf.keras.optimizers.Adam(learning_rate=0.1)
var = tf.Variable(1.0)
opt.minimize(loss,[var])
var.numpy() # 0.90001

1
2
3
4
5

← 激活函数前向、反向传播→