降维

在[[3. 特征工程]]中，我们通过过滤法和嵌入法试图减少特征数量从而提高运算性能，这点被称为降维，这本章节中，我们会深入探讨降维究竟如何实现

# 维度

维度经常挂嘴边，但却有不同含义，以鸢尾花数据集为例 load_iris().data.shape返回的是(150,4)，这说明在数据角度看，数据是二维数组。

我们通过pd.DataFrame(load_iris().data)后看到，在特征矩阵角度看，实际上数据是四维的（因为有4个特征）

# PCA降维

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA

x = load_iris().data
y = load_iris().target

# 调用PCA
pca = PCA(n_components=2)
pca = pca.fit(x)
x_dr = pca.transform(x)

x_dr[:,0]

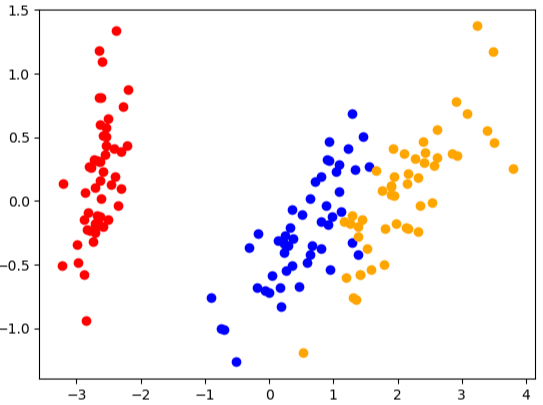
plt.scatter(x_dr[y == 0,0],x_dr[y == 0,1],c="red")
plt.scatter(x_dr[y == 1,0],x_dr[y == 1,1],c="blue")
plt.scatter(x_dr[y == 2,0],x_dr[y == 2,1],c="orange")
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

avatar

# 查看降维后每个新特征向量上所带的信息量大小
pca.explained_variance_
# array([4.22824171, 0.24267075])

# 查看降维后每个新特征向量所占信息占原数据总信息量的百分比
pca.explained_variance_ratio_
# array([0.92461872, 0.05306648])

pca.explained_variance_ratio_.sum() # 0.9776852063187951

1
2
3
4
5
6
7
8
9

从上述鸢尾花数据集在PCA上的表现得知，最终的可解释性方差率之和为0.97，即有0.03不可避免地遗失了，但也已经很高了，特征减少一半，信息却能保留97%

# 学习曲线

再一次，再一次不可避免地用到了学习曲线，虽然笨拙，但却有效。之前使用学习曲线是检测最佳的K值，而如今在PCA中同样的概念出现了，我们需要知道当n_components取何值时，能够得到最高的效率？

score = []
for i in range(1,4):
    pca = PCA(n_components=i)
    d = pca.fit_transform(x)
    score.append(pca.explained_variance_ratio_.sum())

plt.plot(range(1,4),score)
plt.show()

1
2
3
4
5
6
7
8

但实际上，PCA十分先进，你可以在n_components填入mle，这样他会帮你选

# 其他参数

除了上述mle参数，还能直接输入[0,1]之间的浮点数，告诉PCA你期望的总解释性方差占比，也就是说，你希望最终保留多少百分比的信息量，如果你想保留97%，就填写0.97

pca_f = PCA(n_components=0.97,svd_solver="full")
pca_f = pca_f.fit(x)
x_f = pca_f.transform(x)

pca_f.explained_variance_ratio_ # array([0.92461872, 0.05306648])

1
2
3
4
5

由此可见，实际上PCA比起[[3. 特征工程]]提到的过滤法和嵌入法而言更加强大，但他也有缺点，即新特征矩阵不具备可读性，降维后的特征不是原本特征矩阵中任何一个特征，因此我们无法判断

← 特征工程逻辑回归→